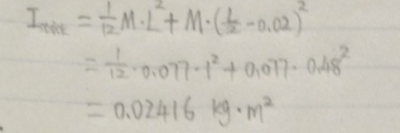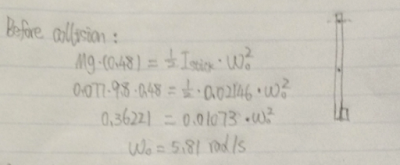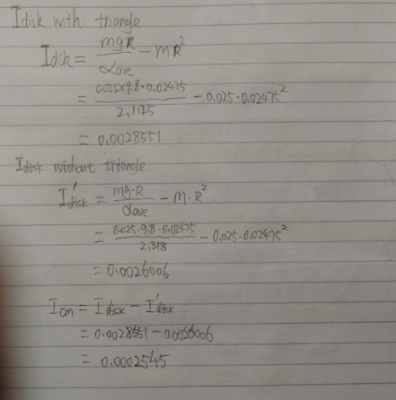Lab 20
Purpose:Derive expressions for the period of various physical verify your prediction periods by experiment.
Apparatus:
1)A photo gate determine the period of the oscillation.
2)A laptop with logger pro
3)Holder that can fix the object do the pendulum.
4)This set up can find the period of each object oscillating.
Steps:
1)A photo gate determine the period of the oscillation.
2)A laptop with logger pro
3)Holder that can fix the object do the pendulum.
4)This set up can find the period of each object oscillating.

1. Find isosceles triangle, a semicircular plate, and a ring, then do five different experiments. At each experiment, set top and bottom as pivot on triangle and semicircular plate, and ring.
2.Experiments
Do five each experiments with triangle, ring, and circular.
Fix the triangle, ring or circular at the pivot point then release it at some very small angle and let it go and using the laptop to collect their period.
This is how it will looks like when doing a experiment.
Record the period of each experiment and mark it for confusing.
3. Prediction
To predict the period of them, Finding the moment of inertia and set up the equation of oscillation then get the angular velocity, and that's how to find out the period.
1)For each with different pivot, they have different moment of inertia. Using the parallel axis theorem to find I.
First of all, find the center of mass and calculate the moment of inertia of center of mass as pivot.Then, using the parallel axis theorem to find the moment of inertia of them.
2)After knowing the moment of inertia, it's very easy to set up the oscillation equation.
(Note:For the oscillation equation, we need to find out the a smililar equation such like a = -kx)
Knowing that Torque = (moment of inertia)* (angular acceleration)
The torque is obvious with only gravity, and the angular acceleration can be represent with some angle.
Also, the angular velocity w^2 = k, and period T = 2*pi/w
And this how to find period.
Example:
Here is some example of this lab.
1.Experiment results
Those are the period of each experiment.
1)First one is the triangle with bottom as pivot, and it gives period T=0.604s.
2)Second one is the triangle as top with pivot.
Period T = 0.6996s

2. Prediction
In order to find the moment of inertia, it's necessary to find the moment of inertia of center of mass.
1) Triangle
- This is how to find the center of mass of iso triangle
- This is how to find the moment of inertia of center of mass
- Using parallel-axis theorem to find the moment of inertia of different pivot.

Uncertainty of the period is less than 1 percent.
2) Semicircular plate:
- This is how to find the center of mass of Semicircular plate
- This is how to find the moment of inertia of center of mass
- Using parallel-axis theorem to find the moment of inertia of different pivot.
- Then using all the results to find the period.
Uncertainty of the period is less than 1 percent.

1. Find isosceles triangle, a semicircular plate, and a ring, then do five different experiments. At each experiment, set top and bottom as pivot on triangle and semicircular plate, and ring.
2.Experiments
Do five each experiments with triangle, ring, and circular.
Fix the triangle, ring or circular at the pivot point then release it at some very small angle and let it go and using the laptop to collect their period.
This is how it will looks like when doing a experiment.
Record the period of each experiment and mark it for confusing.
3. Prediction
To predict the period of them, Finding the moment of inertia and set up the equation of oscillation then get the angular velocity, and that's how to find out the period.
1)For each with different pivot, they have different moment of inertia. Using the parallel axis theorem to find I.
First of all, find the center of mass and calculate the moment of inertia of center of mass as pivot.Then, using the parallel axis theorem to find the moment of inertia of them.
2)After knowing the moment of inertia, it's very easy to set up the oscillation equation.
(Note:For the oscillation equation, we need to find out the a smililar equation such like a = -kx)
Knowing that Torque = (moment of inertia)* (angular acceleration)
The torque is obvious with only gravity, and the angular acceleration can be represent with some angle.
Also, the angular velocity w^2 = k, and period T = 2*pi/w
And this how to find period.


1)For each with different pivot, they have different moment of inertia. Using the parallel axis theorem to find I.
First of all, find the center of mass and calculate the moment of inertia of center of mass as pivot.Then, using the parallel axis theorem to find the moment of inertia of them.
2)After knowing the moment of inertia, it's very easy to set up the oscillation equation.
(Note:For the oscillation equation, we need to find out the a smililar equation such like a = -kx)
Knowing that Torque = (moment of inertia)* (angular acceleration)
The torque is obvious with only gravity, and the angular acceleration can be represent with some angle.
Also, the angular velocity w^2 = k, and period T = 2*pi/w
And this how to find period.
Example:
Here is some example of this lab.
1.Experiment results
Those are the period of each experiment.
1)First one is the triangle with bottom as pivot, and it gives period T=0.604s.
2)Second one is the triangle as top with pivot.
Period T = 0.6996s

2. Prediction
In order to find the moment of inertia, it's necessary to find the moment of inertia of center of mass.
1) Triangle
- This is how to find the center of mass of iso triangle
- This is how to find the moment of inertia of center of mass
- Using parallel-axis theorem to find the moment of inertia of different pivot.

Uncertainty of the period is less than 1 percent.
2) Semicircular plate:
- This is how to find the center of mass of Semicircular plate
- This is how to find the moment of inertia of center of mass
- Using parallel-axis theorem to find the moment of inertia of different pivot.
- Then using all the results to find the period.
Uncertainty of the period is less than 1 percent.
3) Ring:
This is how to find the moment of inertia of total
Then using all the results to find the period

After comparing the experiments results and prediction results.
Uncertainty of them are less 1 percent off.
Conclusion:
This lab is about physics pendulum which gives period in experiment and in prediction. To finish this experiments we set up the equipment and find the period in experiment and compare it with the result we got in prediction.
Given the uncertainty is very small, and results are good.

After comparing the experiments results and prediction results.
Uncertainty of them are less 1 percent off.
Uncertainty of them are less 1 percent off.
Conclusion:
This lab is about physics pendulum which gives period in experiment and in prediction. To finish this experiments we set up the equipment and find the period in experiment and compare it with the result we got in prediction.
Given the uncertainty is very small, and results are good.
Given the uncertainty is very small, and results are good.