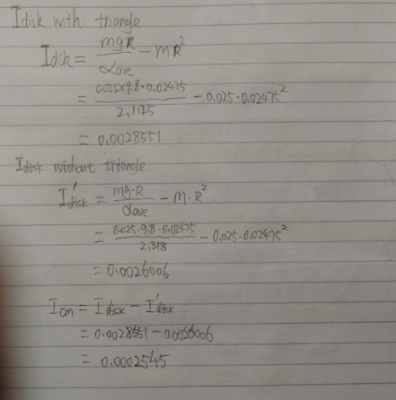Lab 18
Purpose: To determine the moment of inertia of a right triangular thin plate around it's center of mass, for two perpendicular orientations of the triangle.
How to find out moment of inertia of right triangular is what about of this lab. I am going to use one specify equipment to do it today.
Why we chose this equipment because it can give the angular acceleration of the disk. By knowing the angular acceleration , we can use the formula I = a * r calculate the moment of inertia. Thus, The moment of inertia of triangular is the moment of inertia of disk with triangular minus the moment of inertia of disk without the triangular.
Why we chose this equipment because it can give the angular acceleration of the disk. By knowing the angular acceleration , we can use the formula I = a * r calculate the moment of inertia. Thus, The moment of inertia of triangular is the moment of inertia of disk with triangular minus the moment of inertia of disk without the triangular.
Connecting the top disk to computer only and set the disk will spin independently and bottom one stops.
Change the disk to 200 counts per rotating.
weight of disk is 1.36 kg
radius of disk is 0.0625 m
hanging mass is 0.025 kg
Large pulley radius is 0.0495 m.
Triangular long side b = 0.1485 m
Triangular short side a = 0.098 m
weight of triangular 0.455 kg
Those data will be used on next steps.
Triangular short side a = 0.098 m
weight of triangular 0.455 kg
Those data will be used on next steps.
turn on the air so the top disk can rotate, then Start collect on the computer and record the radius and distance on computer.
Those are two experiment should be down, one triangular is at right, one is at bottom.
Part 1
Part 1 is to find out the moment of inertia with those two pose around it's center of mass.
To find out the moment of inertia.
To find out the moment of inertia.
do three experiment, one is without triangular, one is with triangular, and another one is with triangular with different face.
Record the up and down angular acceleration.
Because disk have friction, so up and down accelerations will be different.

By using this equipment, we can find the Angular acceleration up and down with three different condition.
And then use them to find the moment of inertia of disk with those different conditions.
That's equation we use to find out the moment of inertia.
Why we need to find out the moment of inertia is that The moment of inertia of triangular is the moment of inertia of disk with triangular minus the moment of inertia of disk without the triangular.
so we can find the uniform triangular by using this method.
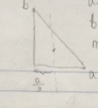 Then collect the data.
Then collect the data.
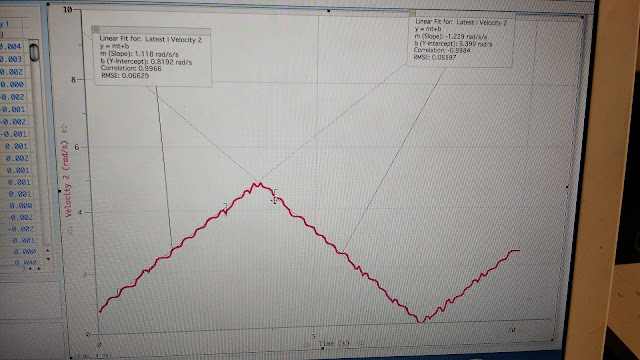
Those graphs are the one without triangular and one with triangle with long side pointing up.
They are angular velocity vs time graph. So the slope of the line are angular acceleration.
Plug the data into the function which can find the moment of inertia
After calculate, moment of inertia of disk with triangular is 0.0028551 kg*m^2
the moment of inertia of disk without the triangular is 0.0026006
Therefore, moment of inertia of triangular rotating aroung the center of mass is 0.0002545 kg * M ^2
Using the same method, find out the another condition's moment of inertia of triangular.
So the moment of inertia of triangular in this pose is 0.0054888 kg* m^2.
In part 1, I obtain the two different moment of inertia around it's center of mass which are 0.0054888 kg* m^2 and 0.0002545 kg * M ^2.
If without the experiment, it's very difficult to find out the moment of inertia around it's center of mass, so need to change the way to calculate them.
If not around the center of mass but around one side.
By around the one edge of the triangular.

it's easy to find I paralle axis and M(d).; thus, the moment of inertia around it's center of mass is just I paralle axis - M(d)
To find I paralle axis and M(d).
After calculation
Moment of inertia around center of mass is just the (1/18) *M* a^2 for this
another will be (1/18) *M* b^2
So for the first one

Moment of inertia around center of mass is 0.000242768 kg* m^2
Uncertainty compare to the value got on the experiment is 4.8 % off.
Another one:


Moment of inertia around center of mass is 0.000557432 kg* m^2
Uncertainty compare to the value got on the experiment is 1.53 % off.
That's equation we use to find out the moment of inertia.
Why we need to find out the moment of inertia is that The moment of inertia of triangular is the moment of inertia of disk with triangular minus the moment of inertia of disk without the triangular.
so we can find the uniform triangular by using this method.
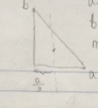 Then collect the data.
Then collect the data.Those graphs are the one without triangular and one with triangle with long side pointing up.
They are angular velocity vs time graph. So the slope of the line are angular acceleration.
Plug the data into the function which can find the moment of inertia
After calculate, moment of inertia of disk with triangular is 0.0028551 kg*m^2
the moment of inertia of disk without the triangular is 0.0026006
Therefore, moment of inertia of triangular rotating aroung the center of mass is 0.0002545 kg * M ^2
Using the same method, find out the another condition's moment of inertia of triangular.
In part 1, I obtain the two different moment of inertia around it's center of mass which are 0.0054888 kg* m^2 and 0.0002545 kg * M ^2.
Part 2
Part two is to test our results.If without the experiment, it's very difficult to find out the moment of inertia around it's center of mass, so need to change the way to calculate them.
If not around the center of mass but around one side.
By around the one edge of the triangular.
it's easy to find I paralle axis and M(d).; thus, the moment of inertia around it's center of mass is just I paralle axis - M(d)
To find I paralle axis and M(d).
After calculation
Moment of inertia around center of mass is just the (1/18) *M* a^2 for this
another will be (1/18) *M* b^2
So for the first one

Moment of inertia around center of mass is 0.000242768 kg* m^2
Uncertainty compare to the value got on the experiment is 4.8 % off.
Another one:


Moment of inertia around center of mass is 0.000557432 kg* m^2
Uncertainty compare to the value got on the experiment is 1.53 % off.
Conclusion:
This is the lab about how to find out the moment of inertia of a uniform triangular rotating about it's center of mass. By using formula and measurement, we find the experiment value and compare with the prediction value to see how well the results are. With friction, mistakes, and not advanced equipment our results are off by 1.53% and 4.8% are good results.